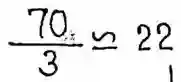Graph Theory is a KTU 2019 Scheme course for S4 CSE students. Here we provide the solved answer key for the Model question paper provided in the syllabus. Why should we solve the model question paper? Graph theory is introduced in the 2019 scheme of KTU. So it is important to solve the model questions in the new pattern. MAT 206 begins with the basics of mathematical logic and logical thinking.
Here we present model questions that cover many topics related to the field of graph theory. In particular, it incorporates a number of algorithmic techniques for determining the structure of graphs and their algorithm representations of the real world. In particular, they will look at graphs that represent logical details and build algorithms on the basis of the mathematical structure of this information.
Before moving to the Answer key we can understand the main aim of this course is to give an in-depth understanding of basic results and facts about graphs and their representations in the light of the central role played by graphs in applied problems.
| Board | KTU |
| Scheme | 2019 New Scheme |
| Year | Second Year |
| Semester | S4 Computer Science |
| Subject | MAT 206 | Graph Theory Solved Model Question Paper |
| Type | Model Question Paper Solved |
| Category | KTU S4 Computer Science |
To fulfil our mission, we try hard to give you qualified and updated study materials. Here is the answer key for the KTU Graph Theory MODEL QUESTION PAPER in the syllabus. Study well & don't forget to share with your friends...
--------------------------------------------------------
Graph Theory Model Question Paper Solved | 2019 Scheme
APJ ABDUL KALAM TECHNOLOGICAL UNIVERSITY FOURTH SEMESTER B.TECH DEGREE EXAMINATION
Course Code: MAT 206
Course name: Graph Theory
Max Marks: 100
Duration: 3 Hours
PART-A
(Answer All Questions. Each question carries 3 marks)
1. Construct a simple graph of 12 vertices with two of them having degree 1, three having degree 3 and the remaining seven having degree 10. (3)
Ans:
Sum of degree = 2e
Two of them have degrees 1
Three of them have degrees 3
Seven of them have degrees 10
So, 2×1+3×3+7×10 = 2e
2+9+70 = 2e
81 = 2e
e = 81/2
= 40.5
The number of edges 40.5 is not possible, so construction is not possible
2. What is the largest number of vertices in a graph with 35 edges, if all vertices are of degree at least 3? (3)
Ans:
Here Sum of degree = 2e
Sum of degree = 2 × 35 = 70
All vertices having a degree of at least 3 means 
vertices having degree 3 and 1 vertex having degree 4
So the number of vertices = 22+1
= 23
3. Define an Euler graph. Give an example of an Eulerian graph that is not Hamiltonian (3)
Ans:
Euler Graph
A connected graph G is said to be Euler, If there is a closed trial includes Every edge of the graph.
Eg: Euler but not Hamiltonian
4. Give an example of a strongly connected simple digraph without a directed Hamiltonian path. (3)
Ans: Out of Syllabus
5. What is the sum of the degrees of any tree of n vertices? (3)
Ans: Sum of the degree of any tree = 2^(n-1)
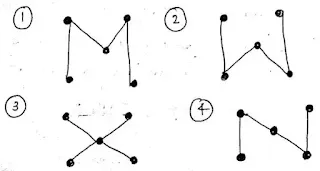
6. How many spanning trees are there for the following graph (3)
Ans:
Spanning trees are :
7. Show that in a simple connected planar graph G having V-vertices, E-edges, and no triangles E <= 3V - 6. (3)
Ans:
If G is simple
2E ≥ 3F
=
2E / 3 ≥ F
By Euler's Formula
V+F-E = 2
V- 2E / 3 - E ≥ 2
3V + 2E-3E ≥ 6
E ≤ 3V – 6
Hence It Proved
8. Let G be the following disconnected planar graph. Draw its dual G* and the dual of the dual (G*)* (3)
Ans:
9. Consider the circuit matrix B and incidence matrix A of a simple connected graph whose columns are arranged using the same order of edges. Prove that every row of B is orthogonal to every row of A? (3)
Ans:
Out of Syllabus
10. A graph is critical if the removal of any one of its vertices (and the edges adjacent to that vertex) results in a graph with a lower chromatic number. Show that Kn is critical for all n > 1. (3)
Ans:
Suppose K3
Chromatic number = 3
By removal of one vertex, chromatic number = 2
So k3 is critical
Kn is Critical For n > 1
PART-B
(Answer any one question from each module. Each question carries 14 Marks)
11. a) Prove that any simple graph with at least two vertices has two vertices of the same degree. (6)
b) Prove that in a complete graph with n vertices there are (n-1)/2 edge-disjoint Hamiltonian circuits and n >= 3 (8)
Ans 11 (a):
Ans 11 (b):
OR
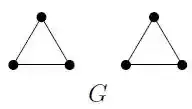
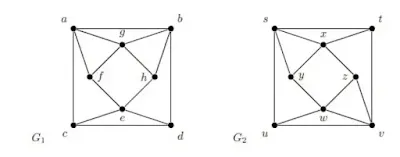
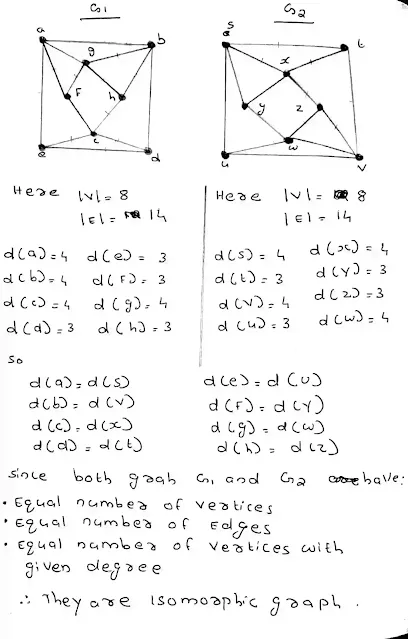
12. a) Determine whether the following graphs G1 = (V1, E1) and G2 = (V2, E2) are isomorphic or not. Give justification. (6)
b) Prove that a simple graph with n vertices and k components can have at most (n-k) (n-k+1)/2 edges (8)
Ans 12 (a):
Ans 12 (b):
13 a) Let S be a set of 5 elements. Construct a graph G whose vertices are subsets of S of size 2 and two such subsets are adjacent in G if they are disjoint.
i. Draw the graph G.
ii. How many edges must be added to G in order for G to have a Hamiltonian cycle? (8)
b) Let G be a graph with exactly two connected components, both being Eulerian. What is the minimum number of edges that need to be added to G to obtain an Eulerian graph? (6)
Ans 13 (a):
Ans 13 (b):
OR
14 a) Show that a k-connected graph with no Hamiltonian cycle has an independent set of size k + 1. (8)
b) i. Let G be a graph that has exactly two connected components, both being Hamiltonian graphs. Find the minimum number of edges that one needs to add to G to obtain a Hamiltonian graph.
ii. For which values of n the graph Qn (hyper-cube on n vertices) is Eulerian. (6)
15 a) A tree T has at least one vertex v of degree 4, and at least one vertex w of degree 3. Prove that T has at least 5 leaves. (5)
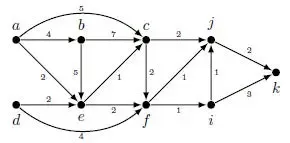
b) Write Dijkstra’s shortest path algorithm. Consider the following weighted directed graph G. (9)
Find the shortest path between a and every other vertex in G using Dijkstra’s shortest path algorithm.
Ans 15 (a):
Let T be a tree
Suppose V has degree 4
W has degree 3
V have degree 4 ⟹ V connected 4 edges
W have degree 3 ⟹ W connected 3 edges
⟹ Minimum, it has 6 edges
⟹ at least 5 leaves
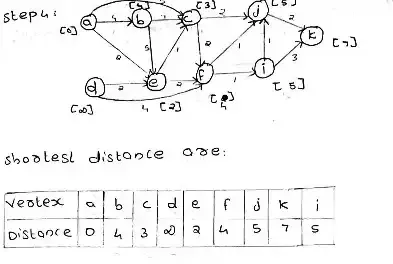
Ans 15 (b):
Dijkstra's Algorithm
This Algorithm is used to find the shortest distance from one vertex to all other vertexes
Step 1: Draw graph with weighted edge
Step 2: Fix a starting vertex
Step 3: Mark distance on initial vertex as ' 0 ' and all other vertexes as ' ∞ '
Step 4: Update all vertex with the shortest distance from the initial vertex
if d(u) + c(u,v) < d(v) then
d(u) + c(u,v) = d(v)
Step 5: Continue this process till all vertex updates
OR
16 a) Define pendent vertices in a binary tree? Prove that the number of pendent vertices in a binary tree with n vertices is (n+1)/2. (5)
b) Write Prim’s algorithm for finding minimum spanning tree. Find a minimum spanning tree in the following weighted graph, using Prim's algorithm. (9)
Determine the number of minimum spanning trees for the given graph.
Ans 16 (a):
The leaf vertex (also the hanging vertex) is a vertex with one degree. ... The simple vertex is that its neighbors form a cluster: all two neighbors are close by. A universal vertex is the vertex next to all the other vertex in the graph.
The number of vertices of odd degree in an undirected graph is even,(N-1) is even. Therefore, n is odd. Let p be the number of pendant vertices.
2+p+3(n- p-1) = 2(n-1)
or, 3n-2n-3+4 = 2p
or, 2p = n+1
or, P = (n+1)/2
Hence, the number of pendant vertices is (n+1)/2.
Ans 16 (b):
Primes Algorithm
This algorithm is used to find the minimum spanning tree of a graph
Step 1: Draw graph with weighted edges
Step 2: Fix a starting vertex
Step 3: Mark an edge with minimum weight from starting index
Step 4: Mark another Edge with minimum weight from the second vertex and previous vertex
Step 5: Continue this process till all vertex occurs once and without forming cycles
17 a) i. State and prove Euler's Theorem relating the number of faces, edges and vertices for a planar graph.
ii. If G is a 5-regular simple graph and |V| = 10, prove that G is non-planar. (9)
b) Let G be a connected graph and e an edge of G. Show that e is a cut-edge if and only if e belongs to every spanning tree. (5)
Ans 17 (a): (i)
Euler's Theorem
If G is a connected plane graph with V- vertices, E- edges, F- face then V+F-E=2
Proof
If G is a tree
F=1
E=v-1
Then V + F - E = 2
= V + 1- ( v - 1)
= V-V+2
= 2
It is true
If G is not a tree
By mathematical induction, Assume it is true for V vertices E edges F faces
ie; V + F - E = 2
Then we have to prove, It is true for E-1 edges then
E = E - 1
F = F - 1
V = V
Then V + F - E = 2
= V+(F-1)-(E-1)
= V+F-1-E+1
= V+F-E
= 2
Hence it is True and it is prooved
OR
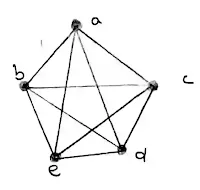
18 a) State Kuratowski's theorem, and use it to show that the graph G below is not planar. Draw G on the plane without edges crossing. Your drawing should use the labelling of the vertices given. (9)
b) Let G be a connected graph and e an edge of G. Show that e belongs to a loop if and only if e belongs to no spanning tree. (5)
Ans 18 (a):
Kuratowski's Theorem
A graph is planar if and only if it does not contain a subgraph homeomorphic to K5 or K3
Proof:
Given graph is isomorphic to K5. So not Planar.
K5
Ans 18 (b): Out Of Syllabus
19 a) Define the circuit matrix B(G) of a connected graph G with n vertices and e edges with an example. Prove that the rank of B(G) is e-n+1 (7)
b) Give the definition of the chromatic polynomial PG(k). Directly from the definition, prove that the chromatic polynomials of Wn and Cn satisfy the identity PWn(k) = k PCn-1 (k – 1). (7)
Ans 19 (a):
Circuit Matrix
A Circuit matrix is a m x n matrix where
n = No of circuit
m = No of edges
It is defined as Cij = 1, If jth edge belongs to the ith circuit
= 0, Otherwise
Proof
The rank of the circuit matrix is e-n+1
(e - number of edges, v - number of vertices)
Let's take
A = incidence matrix of G [rank=n-1]
B = Circuit matrix of G
We have A.B' ≅ O (mod 2)
By 'Sylvester's theorem
rank (A) +rank (B) = e
rank (B) ≤ e - rank (A)
rank (B) ≤ e - (n-1)
rank (B) ≤ e - n+1 ------------ 1
For any connected graph
rank(B) ≥ e-n+1 ------------ 2
From 1 and 2
rank( B) = e-n+1
Ans 19 (b):
Chromatic Polynomial
Chromatic Polynomial counts the number of Graph covering as a function of the number of colours
OR
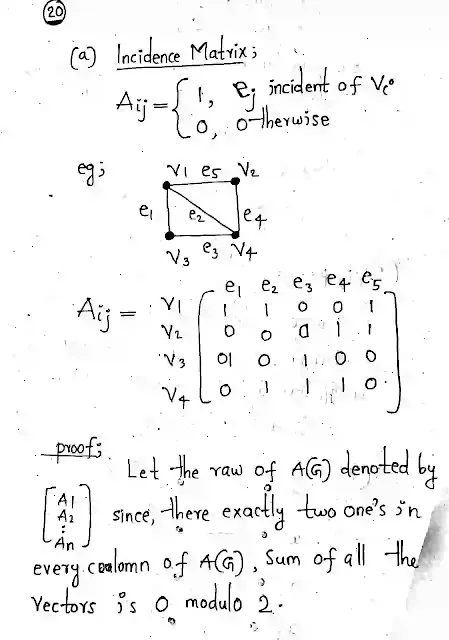
20 a) Define the incidence matrix of graph G with an example. Prove that the rank of an incidence matrix of a connected graph with n vertices is n-1. (4)
b) i. A graph G has chromatic polynomial PG(k) = k4-4k3+5k2-2k. How many vertices and edges does G have? Is G bipartite? Justify your answers.
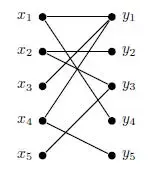
ii. Find a maximum matching in the graph below and use Hall's theorem to show that it is indeed maximum. (10)
Ans 20 (a), (b):
--------------------------------------------------------
You May Like :
- KTU S4 CSE Graph Theory Notes
- KTU S4 CSE Computer Organization and Architecture Notes
- KTU S4 CSE Database Management System Notes
- KTU S4 CSE Operating System Notes
- KTU S4 CSE Design and Engineering Notes
- KTU S4 CSE Constitution Of India Notes
We hope the given KTU S4 MAT 206 Graph Theory Solved Model Question based on the 2019 scheme will help you in your upcoming Examinations. If you like this share it with your friends.
"Share KeralaNotes.Com with your friends"
We have solved the Graph theory exemplar question paper in the syllabus for S4 CSE students. Explain all the questions as asked in the sample question paper for this KTU 2019 syllabus lesson. Graph Theory model question paper is for CSE S4 students preparing for the KTU 2019. Examination course. Includes all the chapters in the KTU 2019 syllabus Theory. preparing for the KTU 2019 exam in Graph theory, this questionnaire will help you. Graph Theory is one of the most important topics in the KTU syllabus. Model question paper question bank of graph theory will definitely help you to score good marks with the Answer key provided
If you have any queries regarding the KTU S4 Computer Science (CSE) Study Materials, drop a comment below and we will get back to you at the earliest.
